究進塾では、Youtubeチャンネルにて解説動画を公開しておりますが、先日視聴者の方より、コメント欄へご質問を頂きました。

ご質問頂いたのは、江口先生の解説動画「電磁気学 第9回、コンデンサーとその静電容量」の例題解説に関する内容です。

そこで今回は、動画解説の内容と、ご質問および先生からの回答をご紹介いたします。

江口先生の動画解説

はじめに
動画で解説をしている内容をご紹介します。当記事では公式等は掲載しておりますが、各章ともそれに至るまでの解説部分は省略しているところがございます。
詳細に知りたい、理解を深めたいという方はぜひ動画をご覧いただき、江口先生の授業の雰囲気も一緒に掴んでいただければと思います。

 江口和弘講師
「電磁気学 第9回 静電容量（コンデンサー）」
（所要時間 51:29 ）

動画目次
1. コンデンサー（0:20～）
2. 静電容量の例（2:30～）
3. コンデンサーの接続（11:14～）
4. 静電容量のΔ-Y変換（14:59～）
5. コンデンサーが蓄えるエネルギー（17:57～）
6. コンデンサーの両極に働く力（19:17～）
7. 例題（21:38～）
（分数をクリックすると該当箇所が別窓で開きます）

①コンデンサーとは
■2つの導体を対置して電荷を蓄えるようにしたもの
■1つの孤立導体の場合はこの孤立導体に電荷を蓄える

このように電荷を蓄える仕組みを持ったものを「コンデンサー」と呼び、コンデンサーがどれだけ電荷を蓄える能力を持っているかを表したのが「静電容量」という数字です。

⇒孤立導体の静電容量
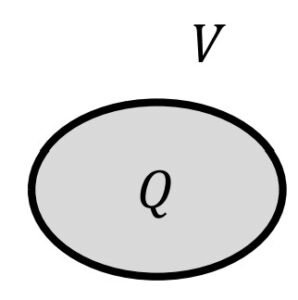孤立導体に電荷Qが蓄えられているときに電位Vであるときの静電容量は\(C=\frac{Q}{V}\)、つまりQ=CVとなります。Cの量は同じ電位（V）を与えられた時にどれだけの電荷（Q）が蓄えられるかを表している数字であり、Cが大きいほど同じ電圧を印加した時にたくさんの電荷が蓄えられることを表しています。

⇒2導体間の静電容量
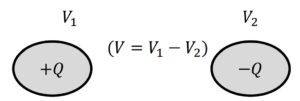片方の導体に+Qを与え、もう一方に-Q、逆方向の電荷を与えます。そのときの電位がこのV₁、V₂になっていたとすると、このときの静電容量Cは、このQをこの間の電位差で終わったということになります。V₁、V₂は電位差を表しているため、電位差に書き換えると、\(C=\frac{Q}{V₁-V₂}=\frac{Q}{V}\)となり、孤立導体の場合とほぼ同じ式になります。
ただし2導体間の場合は電荷+Q、-Qを与えます。そのときの電位Vというのは、2導体間の電位差を考える、というところが違います。

②静電容量の例
代表的な例を4つ紹介します。基本的な計算の流れは、動画の江口先生の説明をご覧ください。
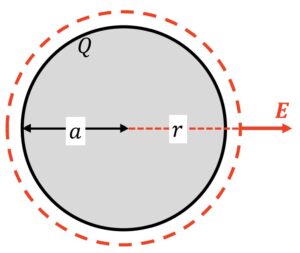
■孤立導体球（半径a、無限遠に対して）4:27より解説
C=4πε₀a

■平行平板コンデンサ―（面積S、間隔d）5:50より解説
\(C=\frac{ε₀S}{d}\)

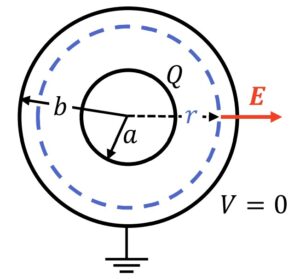
■同心球コンデンサー（内半径a、外半径b、内球絶縁、外球接地）8:06より解説
C=4πε₀\(\frac{ab}{b-a}\)

■同軸円筒コンデンサー（内半径a、外半径b、長さl（l≫a）、内円筒絶縁、外円筒接地）9:35より解説
C=2πε₀\(\frac{l}{log(b/a)}\)

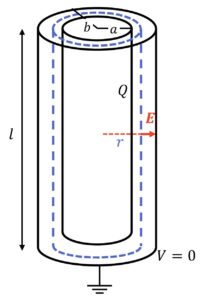
③コンデンサーの接続
この公式は、覚えておいた方が良いものです。
・直列接続：\(\frac{1}{C}\)=\(\frac{1}{C₁}\)+\(\frac{1}{C₂}\)+…+\(\frac{1}{Cn}\)

・並列接続：\( {}C=C_1+C_2+\)… +\( {}C_n\)

公式の説明は動画の解説をご覧ください。ほとんどの場合は直列接続と並列接続を繰り返していくことによって合成容量は計算してできますが、回路の構成によってはできないものもあります。

④静電容量のΔ-Y変換

直並列接続で計算できない回路の構成の場合によく使うものとして「Δ-Y（デルタ-スター）変換」があります。

Δ（デルタ）接続
⇒三角形に3つ接続したもの
Y（スター）接続
⇒Y字型に接続したもの

これで、この2つのコンデンサーの容量の間にどういう関係があるかを調べてみると、以下のようになります。

A-B間：C₃+\(\frac{C₁C₂}{C₁+C₂}\)=\(\frac{CaCb}{Ca+Cb}\)

B-C間：C₁+\(\frac{C₂C₃}{C₂+C₃}\)=\(\frac{CbCc}{Cb+Cc}\)

C-A間：C₂+\(\frac{C₃C₁}{C₃+C₁}\)=\(\frac{CcCa}{Cc+Ca}\)

連立方程式で解けますが少し厄介な形をしているので、連立方程式を解くことには変わりありませんが、逆数をとると比較的計算しやすくなります。計算結果は以下のようになります。

Ca=\(\frac{C₁C₂+C₂C₃+C₃C₁}{C₁}\)

Ca=\(\frac{C₁C₂+C₂C₃+C₃C₁}{C₂}\)

Ca=\(\frac{C₁C₂+C₂C₃+C₃C1}{C₃}\)

これをΔ-Y変換と呼びます。逆にYからΔに変換すると以下のようになります。

C₁=\(\frac{CbCc}{Ca+Cb+Cc}\)

C₂=\(\frac{CcCa}{Ca+Cb+Cc}\)

C₃=\(\frac{CaCb}{Ca+Cb+Cc}\)

このように相互に変換できるということがあります。これを使って合成容量を計算することができます。

⑤コンデンサーが蓄えるエネルギー
孤立導体：U=\(\frac{1}{2}QV\)=\(\frac{1}{2}CV^2\)=\(\frac{1}{2}\)\(\frac{Q^2}{C}\)
コンデンサー（2導体間の場合）：
U=\(\frac{1}{2}\)QV₂-\(\frac{1}{2}\)QV₁=\(\frac{1}{2}\)Q(V₂-V₁)
V₂-V₁というのは電位差Vなので、
V=V₂-V₁
Q=C(V₂-V₁)=CV

高校の物理では、単に公式として出てくるだけだと思います。「なぜこうなるのか」という説明はあまりなされないと思います。

⑥コンデンサーの両極に働く力
■電荷一定のとき
電荷が一定のときはエネルギーを変位方向に取って、微分したものにマイナスがつきます。
\(F_ξ\)=-\(\frac{∂U}{∂ξ}\)=-\(\frac{∂}{∂ξ}\)\((\frac{Q^2}{2C})\)=\(\frac{Q^2}{2C}\)\(\frac{∂C}{∂ξ}\)
■電位一定のとき
今度は電位一定の場合、エネルギーは、U=\(\frac{1}{2}\)\(CV^2\)という形をとります。\(V^2\)が一定です。そうすると、単にこれはCを説明した形になります。
\(F_ξ\)=\(\frac{∂U}{∂ξ}\)=\(\frac{∂}{∂ξ}\)\((\frac{CV^2}{2})\)=\(\frac{V^2}{2}\)\(\frac{∂C}{∂ξ}\)

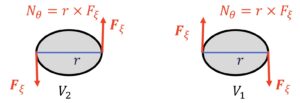それから、逆方向にはたらいてモーメントを発生させる力を、力学では偶力といいます。全く逆向きの力がはたらいてることで力的にはバランスを保っているのですが、ではこのような力がはたらいたときにこの物体がじっとしてるかというと、そうではないわけです。平行移動はしないけれどぐるっと回ってしまいます。このような関係の力を偶力といいます。このときも全く似たような関係が成り立ち、偶力のモーメント（距離×力、N=r×F）を求めてやると、電荷が一定のときは今度は変位距離ξの代わりに回転角θで微分します。電荷一定の場合はマイナスがつき、電位が一定の時はマイナスがつきません。
■電荷一定のとき：\(N_θ\)=-\(\frac{∂U}{∂θ}\)
■電位一定のとき：\(N_θ\)=\(\frac{∂U}{∂θ}\)

⑦例題
コンデンサーには色々な例題があるので、動画の後半はそちらをご紹介しています。例題数は9題と多めになっており、江口先生の解説付きですので、練習にご活用ください。

ご質問内容と解答

ここからは、Youtubeの視聴者の方より、コメント欄に頂いたご質問をご紹介します。
ご質問いただいたのは、3つ目の例題(27:00~)に関する内容です。

■例題と解答

問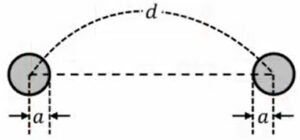： 半径aの2本の極めて長い直線状導線が中心間距離 d (d≫a) を隔てて平行におかれているとき、単位長さあたりの静電容量を求めよ。

解： 単位長さあたりの電荷 ±λ 位置\(x\)における電場　E=\(\frac{λ}{2πε₀}\)\(\frac{1}{x}\)+\(\frac{λ}{2πε₀}\)\(\frac{1}{d-x}\) （Gaussの法則より） 電位差　V=-\(\displaystyle \int_{d-a}^a Edx\)=-\(\frac{λ}{2πε₀}\)\(\displaystyle \int_{d-a}^a\) \((\frac{1}{x}+\frac{1}{d-x})\)\(dx\)=\(\frac{λ}{πε₀}\)log\(\frac{d-a}{a}\) 単位長さあたりの静電容量C=\(\frac{λ}{V}\)=\(\frac{πε₀}{log\lbrace(d-a)/a\rbrace}\)≒\(\frac{πε₀}{log(d/a)}\)

■ご質問
以下が、頂いたご質問の内容です。
「江口先生初めまして。29:30の積分範囲がなぜ(d-a)からaまでなのかがよくわかりません、基準をどこかに取っているのでしょうか」

■ご質問への回答

以下、江口先生からの解答文となります。

********************************************************

ある点の電位の定義は、1[C]の電荷をその点から無限遠まで運ぶとき電場による静電気力がする仕事（あるいは電場からの静電気力に逆らって無限遠からその点まで運ぶ時の仕事）です。

よって、\(x=x_₁\)における電位は、

\(\displaystyle \int_{x_₁}^∞ Edx\) = －\(\displaystyle \int_∞^{x_₁} Edx\).

この例題では、導線は導体なので、内部では\(E=0\)なので、導体は等電位。よって、片方の導線表面ともう一方の導線の表面の間の電位差を求めればよいことになります。

\(V_{x=a} =－\displaystyle \int_∞^a Edx\), \(V_{x=d-a}=－\displaystyle \int_∞^{d-a} Edx\)

よって、電位差は

\(V_{x=a}－V_{x=d-a}=－\displaystyle\int_∞^a Edx －( －\displaystyle\int_∞^{d-a} Edx )\)

\(= －\displaystyle\int_∞^a Edx + ( －\displaystyle\int_{d-a}^∞ Edx) = －\displaystyle\int_{d-a}^a Edx\)

になります。両導体の中心間の電位差を考えて、\(x=d\) から \(x=0\) まで積分しても、\(0≦x≦a,　d – a ≦x≦d\) では \(E=0\) なので、積分しても 0 であり、結果は同じになります。

おわりに

今回の解説紹介は以上となります。いかがでしたでしょうか。

江口先生の電磁気学は、Youtubeで現在第20回までを公開しており、引き続きアップを予定しております。気になる方は、他の内容もぜひご覧ください。

また究進塾では、入塾前に無料で授業の体験をすることができます。受講をしてみたいという方、ご質問のあるは「無料体験授業をご希望の方」からお気軽にご相談ください。事務局を通して、丁寧に対応させていただきます。